Ecological Synchrony
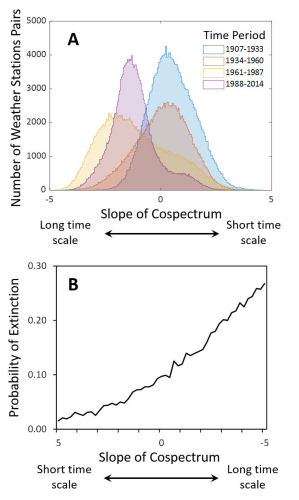 My colleagues and I are using spectral analyses to examine synchrony in the frequency domain. Our goals are (1) to derive new theoretical results, (2) to conduct new laboratory experiments that test our theoretical predictions, and (3) to analyze data from ecological and environmental databases that extend over large geographical areas and extended periods of time. Our results show how total synchrony changes in response to population growth rates, rates of dispersal among populations, and the time scales of environmental variation and environmental correlation. We also found that time scales of environmental correlations are becoming longer, perhaps due to climate change, and that these changes impose an increased risk of extinction for fragmented ecological populations.
My colleagues and I are using spectral analyses to examine synchrony in the frequency domain. Our goals are (1) to derive new theoretical results, (2) to conduct new laboratory experiments that test our theoretical predictions, and (3) to analyze data from ecological and environmental databases that extend over large geographical areas and extended periods of time. Our results show how total synchrony changes in response to population growth rates, rates of dispersal among populations, and the time scales of environmental variation and environmental correlation. We also found that time scales of environmental correlations are becoming longer, perhaps due to climate change, and that these changes impose an increased risk of extinction for fragmented ecological populations.
Spectral Analyses of Population Dynamics
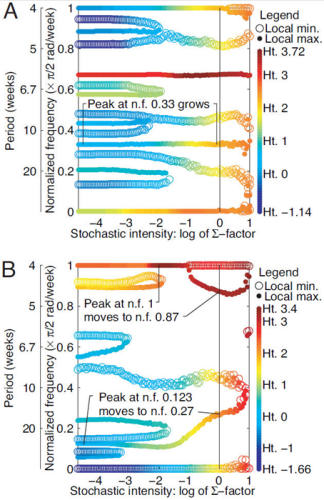 The power spectrum is a powerful mathematical tool that takes a population time series as input and gives as output a plot showing the amount (power) of fluctuation that occurred in the population at each of a range of frequencies. Frequencies at which important oscillations occurred can be read from this plot; they are the frequencies at which peaks in the spectrum occur. The spectrum gives a comprehensive signature of population dynamics. We use controlled laboratory experiments and mathematical models to understand the interaction between environmental variability and intrinsic population nonlinearities. Our findings contribute to understanding how nonlinear population dynamics interact with stochasticity.
The power spectrum is a powerful mathematical tool that takes a population time series as input and gives as output a plot showing the amount (power) of fluctuation that occurred in the population at each of a range of frequencies. Frequencies at which important oscillations occurred can be read from this plot; they are the frequencies at which peaks in the spectrum occur. The spectrum gives a comprehensive signature of population dynamics. We use controlled laboratory experiments and mathematical models to understand the interaction between environmental variability and intrinsic population nonlinearities. Our findings contribute to understanding how nonlinear population dynamics interact with stochasticity.
Nonlinear Population Dynamics
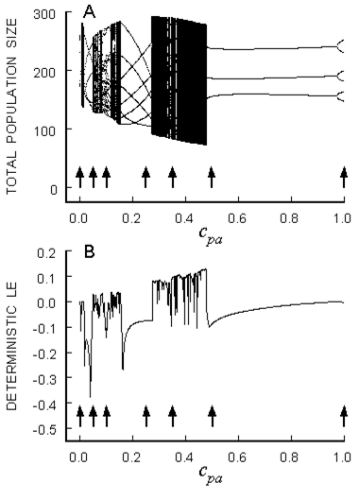 I participate in an interdisciplinary research project that integrates mathematical, statistical, and experimental methods for the investigation of nonlinear population dynamics. Our goal is to provide experimental tests of dynamic behaviors such as periodic cycles, aperiodic orbits, multiple attractors, unstable equilibria with stable and unstable manifolds, chaos, and strange attractors. Laboratory populations of flour beetles of the genus Tribolium are serving as an animal model. For example, we reported an experiment that provided the first convincing example of chaos in ecology. This work also focuses on how stochasticity interacts with nonlinearity to influence population time series.
I participate in an interdisciplinary research project that integrates mathematical, statistical, and experimental methods for the investigation of nonlinear population dynamics. Our goal is to provide experimental tests of dynamic behaviors such as periodic cycles, aperiodic orbits, multiple attractors, unstable equilibria with stable and unstable manifolds, chaos, and strange attractors. Laboratory populations of flour beetles of the genus Tribolium are serving as an animal model. For example, we reported an experiment that provided the first convincing example of chaos in ecology. This work also focuses on how stochasticity interacts with nonlinearity to influence population time series.
Spatially-Mediated Dynamics in Benthic Communities
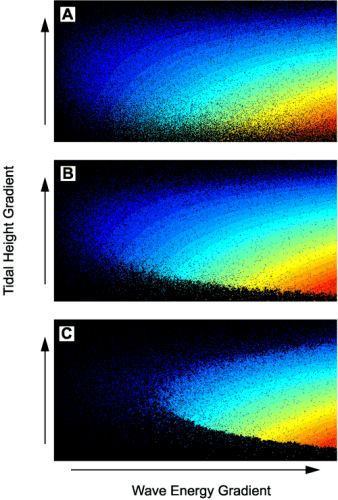 I am part of a research group investigating the dynamics of size-specific predation of mussels by sea stars in rocky intertidal communities. Spatial neighborhood effects in both recruitment and predation play an important role in these dynamics and the strengths of these neighborhood effects vary over gradients of wave energy and tidal exposure. We integrate empirical data into a variety of models of the intertidal zone including stochastic cellular automata, mean field ordinary differential equations, and agent-based models. Simulations of the model generate size frequency distributions over space that can be compared to real patterns from field observations.
I am part of a research group investigating the dynamics of size-specific predation of mussels by sea stars in rocky intertidal communities. Spatial neighborhood effects in both recruitment and predation play an important role in these dynamics and the strengths of these neighborhood effects vary over gradients of wave energy and tidal exposure. We integrate empirical data into a variety of models of the intertidal zone including stochastic cellular automata, mean field ordinary differential equations, and agent-based models. Simulations of the model generate size frequency distributions over space that can be compared to real patterns from field observations.

